5.3. Relation de sous-typage dans le module de types
5.3.1. Sous-typage des C-types
Une hiérarchie structurelle, illustrée dans la figure Hiérarchie des classes de CTypes du début de chapitre, est définie pour les différentes Classes de C-types. Cette hiérarchie permet de structurer les C-types selon leurs caractéristiques. Ainsi, lorsque l'on souhaite ajouter un nouveau C-type, on l'intègrera dans cette hiérarchie pour qu'il hérite des caractéristiques pré-définies (ordonné, construit,...).
Pour typer un slot dans AROM on n'utilisera pas directement une de ces classes. En effet, une variable n'est pas de type discret ou multivalué mais de type entier ou list d'entier de 0 à 120. On utilise non pas les classes de C-type mais des instances de ces classes.
Ce chapitre traite de la relation de sous-typage qui existe entre les instances des C-types. Cette relation est orientée vers les données représentées par les C-types, elle n'est pas maintenue mais elle est vérifiée au cas par cas sur demande. La comparaison des instances se fait pour chaque classe de C-type, c'est pourquoi une définition est donnée pour chacune de ces classes de C-types.
Néanmoins, cette relation est toujours basée sur un même principe qui est l'inclusion ensembliste.
Les CTypes ordonnés n'acceptent que des singletons comme instances, par conséquent le problème de relation de sous-typage des instances de C-type ne se pose pas. Dans le cas où un nouveau CType est intégré dans les C-types ordonnés, cet aspect sera à prendre en compte.
Deux CTypes ordonnés ne peuvent donc pas avoir de super C-type commun.
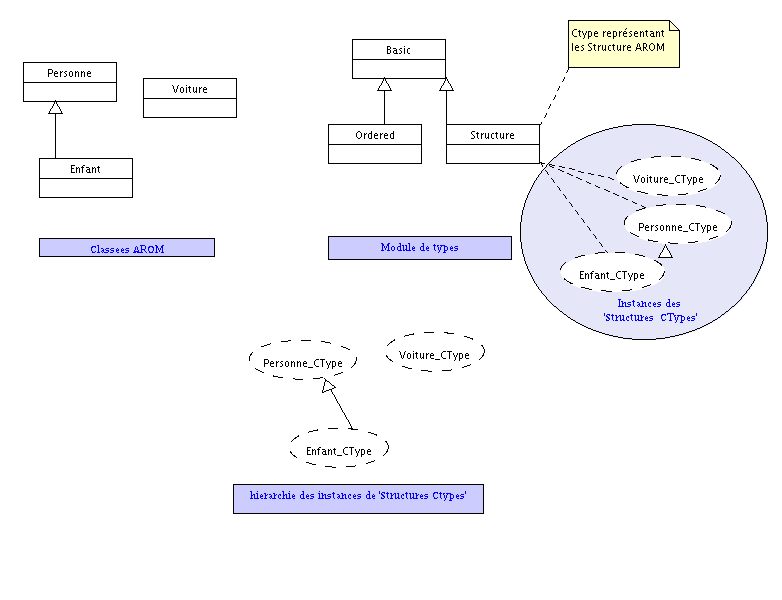
Les StructureCT permettent de typer les structures AROM. Il est donc logique que l'on retrouve la même relation d'ordre que celle des structures. Dans l'exemple ci-dessous, le type Pesonne_CType est le Super C-type de Enfant_CType. Par contre le type Voiture_CType est dissocié des deux autres.
A partir de deux StructureCT il est donc facile de déterminer si il existe un super C-type commun, puisque la hiérarchie des StructureCT est accessible via celle des structures AROM.
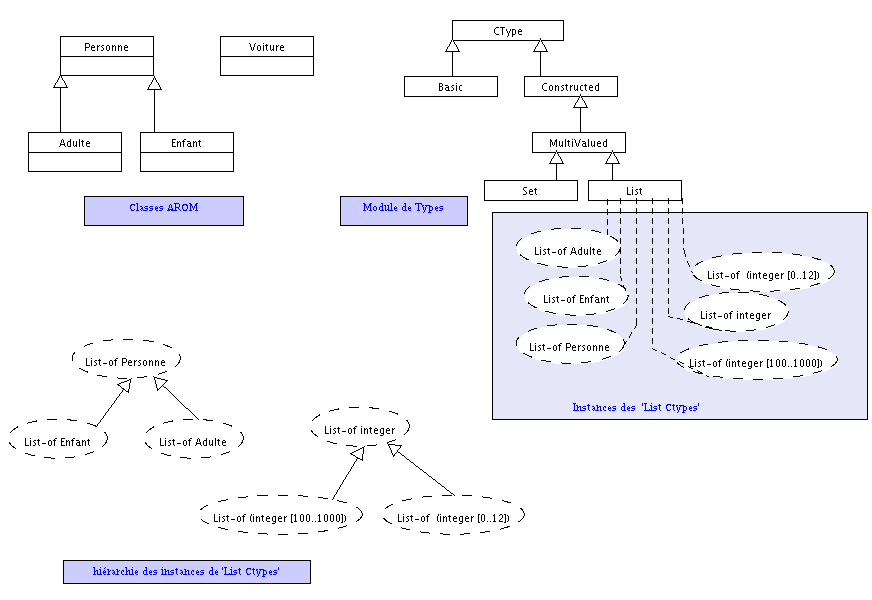
Les MultiValCT, qui se déclinent en ListCT et en SetCT, sont des collections d'objets appartenant à un δ-type donné. La relation de sous-typage de ces C-types est donc la même que celle existante entre les δ-types des éléments. Dans les cas les plus simple, lorsque le δ-type décrit un C-type, les mêmes règles que celles décrites dans cette section sont appliquées. Par exemple, si l'on considère l'exemple qui suit, le type List-of Personne est super C-type de List-of Enfant et List-of Adulte. Pour le cas où les δ-types des éléments de la collection définissent un domaine, la relation de sous-typage des MultiValCT est celle des δ-types, c'est à dire que c'est une relation d'ensembles. Ainsi, le type List-of Integer est super C-type de List-of (Integer [0..12]) et de List-of (Integer [100..1000]). Par contre les deux sous C-types n'ont pas de relation de sous-typage. Voir le chapitre qui suit sur la relation de sous-typage des δ-types pour plus d'informations.
Le Super C-type commun à deux MultiValCT, mv1 et mv2, est un MultiValCT basé sur le super δ-type commun aux δ-types composant mv1 et mv2.
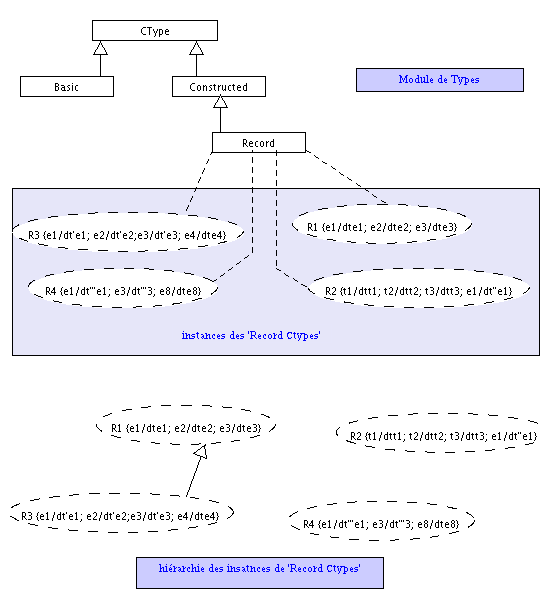
Enfin, il reste les RecordCT qui définissent un ensemble de couples "étiquettes/δ-types". Les StructureCT et les RecordCT ne diffèrent que par le fait que les StructureCT représentent explicitement des structures AROM alors que les RecordCT représentent toute donnée coposée de couple étiquette-δ-type. Les RecordCT sont d'ailleurs utilisés pour représenter les intentions des StructureCT. En effet, une structure est définie par un ensemble de slots ayant un identifiant (nom) et un δ-type. Par conséquent, les mêmes règles de spécialisations que celles des Structures AROM sont utilisées. C'est à dire que pour qu'un RecordCT soit sous C-type d'un autre RecordCT il faut qu'il définisse les mêmes étiquettes et que celles-ci soient associées au même δ-type ou à un sous δ-type. D'autre étiquettes peuvent être définies au niveau du sous C-type.
Dans l'exemple ci-après, le C-type R1 est super C-type de R3 si les δ-types dt'e1, dt'e2 et dt'e3 sont égaux ou sous δ-types de, respectivement, dte1, dte2 et dte3. Par contre, le C-type R2 est entièrement dissocié des autres C-types malgrès la définition de l'étiquette e1. Le C-type R4 ne peut pas non plus aspirer à être un sous C-type de R1 puisqu'il ne définit pas l'étiquette e2.
De la même façon que pour les MultiValCT, il est possible de déterminer un Super C-type commun à deux RecordCT, RecCT1 et RecCT2. Ce RecordCT devra ne définir que les étiquettes communes à RecCT1 et RecCT2. Les δ-types associés à ces étiquettes devront être des super δ-types de ceux associés aux étiquettes de RecCT1 et RecCT2. Un exemple est donné ici:
RecCT1 : e1 / integer [0 .. 20] e2 / string {"julien", "barnabé", "ivan"} e3 / float RecCT2 : e1 / integer [100 .. 2000] e2 / string {"nathalie", "helene", "pierre"} e4 / boolean le RecordCT parent commun minimal à RecCT1 et RecCT2 est : e1 / integer [0 .. 20] U [100 .. 2000] e2 / string {"julien", "barnabé", "ivan", "nathalie", "helene", "pierre"}
5.3.2. Relations de sous-typage des δ-types
De la même façon que pour les C-types, on s'intéresse à la relation de sous-typage des instances de δ-types. La hiérarchie structurelle est identique à celle des C-types et elle est utile pour les utilisateurs désirant ajouter de nouveaux types dans AROM.
Les δ-types sont composés d'un C-type de base et d'un domaine qui est un sous-ensemble du domaine de valeurs décrit par le C-type. Par conséquent, la hiérarchie définit pour les C-types est appliquées ici mais on l'affine en fonction des domaines spécifiés.
Dans tous les cas, quelque soit la catégorie à laquelle on s'intéresse, le δ-type Max, qui représente le même domaine que le C-type auquel il est associé, est au sommet de la hiérarchie, il est super δ-type de tous les autres δ-types appartenant à la même classe. Inversement, le δ-type Min, qui représente l'ensemble vide, est en bas de la hiérarchie. Une description plus précise pour les autres cas de figure est donné pour chaque catégorie de δ-type.
D'une manière générale, la règle de spécialisation appliquée est: Pour qu'un δ-type soit sous δ-type d'un autre, il faut que toutes ses valeurs soient acceptées par le second.
Les DeltaType ordonnés hérite des C-types d'un unique niveau qui est le singleton définit par ces C-types et qui représente le δ-type Max, c'est à dire le super δ-type de tous les autres. Ce niveau définit donc l'ensemble des entiers, des réels, des chaînes de caractères ou des booleens selon le DeltaType considéré.
Les domaines associés aux δ-types ordonnés sont représentés par des listes d'intervalles de valeurs autorisées. Si l'on reprend la règle de spécialisation énoncée ci-dessus, pour qu'un δ-type d2 soit sous type d'un δ-type d1, il faut que le domaine de d2 soit inclus dans le domaine de d1. Par exemple, Integer {[- inf .. 12] U [58 .. 8996]} est super δ-type de Integer {[- inf .. -1002] U [0 .. 10] U [ 789 .. 1000]}
Cette définition permet également de dire que le super δ-type minimum commun à deux δ-types distincts est l'union de ces deux types. De la même façon le sous δ-type maximum commun à deux δ-types distincts est l'intersection de ces deux types. Deux δ-types sont dits distincts si ils ne peuvent pas être hiérarchisés, aucun n'est sous type de l'autre. De plus, par minimum (maximum) on entends le δ-type ayant le moins (plus) de valeurs autorisées.
Les valeurs des StructureCT sont les instances des Structures AROM représentées. Les domaines des StructureDT peuvent donc toujours être représentés par un ensemble d'instances autorisées. En effet, si l'on précise un ensemble d'instances interdites, l'ensemble résultant est l'ensemble de toutes les instances auquel on aura retiré les instances précisées par l'utilisateur. Un StructureDT δts2 définissant un domaine S2 est sous δ-type d'un StructureDT δts1 définissant un domaine S1 si il est possible de déterminer une relation de sous-typage entre les StructureCT qui leur sont associés et si la règle ci-dessous est vrai :
S1 = X (X={x1,...,xn}) S2 = Y (Y={y1,...,ym}) δts2 < δts1 ssi ∀ y ∈ Y, y ∈ X
La relation qui peut exister entre les δ-types δts2 et δts1 n'est pas obligatoirement la même que celle qui existe entre leur C-type, Cs1 et Cs2.
Dans le cas où une relation entre deux δ-types ne peut être déterminé, mais qu'il existe une relation entre les StructureCT qui leur sont associé, il est possible de définir le super δ-type minimum commun. Celui-ci est issu d'un des deux StructureCT associé aux δ-type, celui qui est super type de l'autre, et il a pour domaine l'union des domaines des deux δ-types δts1 et δts2.
Les MultiValDT restreignent les MultiValCT en définissant, d'une part, des domaines sous forme d'ensembles de valeurs autorisées ou interdites et, d'autres part, une cardinalité.
Dans le cas où un domaine de valeurs est définit, la cardinalité n'entre en ligne de compte que lors de l'ajout de valeurs à ce domaine. Un MultiValDT δtmv2 définissant un domaine S2 est sous type d'un MultiValDT δtmv1 définissant un domaine S1 si une des règles ci-dessous est vrai :
S1 = X (X={x1,...,xn}) S2 = Y (Y={y1,...,ym}) δtmv2 < δtmv1 ssi ∀ y ∈ Y, y ∈ XS1 = !X (X={x1,...,xn}) S2 = Y (Y={y1,...,ym}) δtmv2 < δtmv1 ssi a. δtmv1MAX ≥ δtmv2MAX : ∀ y ∈ Y, y ∉ X b. δtmv1MAX < δtmv2MAX : ∀ y ∈ Y, ( y ∉ X && y ∈ δtmv1MAX )S1 = !X (X={x1,...,xn}) S2: !Y (Y={y1,...,ym}) δtmv2 < δtmv1 ssi a. δtmv1MAX ≥ δtmv2MAX : ∀ x ∈ X, ( x ∈ Y ∥ x ∉ δtmv2MAX ) b. δtmv1MAX < δtmv2MAX : Z = δtmv2MAX diff δtmv1MAX ∀ x ∈ X, x ∈ Y && ∀ z ∈ Z, z ∈ YS1 = X (X={x1,...,xn}) S2 = !Y (Y={y1,...,ym}) δtmv2 < δtmv1 ssi a. δtmv1MAX ≥ δtmv2MAX : Z = δtmv2MAX diff Y ∀ z ∈ Z, z ∈ X b. δtmv1MAX < δtmv2MAX : Z = δtmv1MAX diff Y U = δtmv2MAX diff δtmv1MAX ∀ z ∈ Z, z ∈ X && ∀ u ∈ Y, u ∈ Y
Les points iii et iv ci-dessus ne sont pas toujours vérifiable. En effet, le δtmvMAX peut etre infini, si la cardinalité maximum est infini et/ou le nombre d'éléments composant les collections est infini.
Pour déterminer un super δ-type commun (le minimum ?) à deux MultiValDT qui ne sont reliés par le sous-typage, les règles suivantes s'appliquent:
S1 = X (X={x1,...,xn}) S2 = Y (Y={y1,...,ym}) δtMVparent > δtmv1 et δtMVparent > δtmv2 ssi Sparent = S1 ∪ S2 && C-type associé à δtMVparent = 1. C-type associé à δtmv1 si ∀ y ∈ Y, y ∈ δtmv1MAX 2. C-type associé à δtmv2 si ∀ x ∈ X, x ∈ δtmv2MAX 3. Super C-type commun de δtmv1 et δtmv2, sinon.S1 = X (X={x1,...,xn}) S2 = !Y (Y={y1,...,ym}) δtMVparent > δtmv1 et δtMVparent > δtmv2 ssi Z = Y diff X Sparent = !Z, && C-type associé à δtMVparent = 1. C-type associé à δtmv2 si ∀ x ∈ X, x ∈ δtmv2MAX 2. Super C-type commun de δtmv1 et δtmv2, sinon.S1 = !X (X={x1,...,xn}) S2 = !Y (Y={y1,...,ym}) δtMVparent > δtmv1 et δtmv2 ssi Z = (X diff δtmv2MAX) ∪ (Y diff δtmv1MAX) ∪ (Y ∩ X) Sparent = !Z, && C-type associé à δtMVparent = Super C-type commun de δtmv1 et δtmv2.
Dans le point ii ci-dessus, on remarque que ce n'est pas le super δ-type commun qui est définit. En effet, par exemple, dans le cas où S1 ∉ δtmv2 Z = Y et le C-type de δtMVparent et le super C-type de ceux associés à δtmv1 et δtmv2. Par conséquent, tous les éléments de δtmv1 seront inclus dans δtMVparent au lieu des seules éléments de X.
Par contre, si aucun domaine n'est défini, toutes les valeurs du C-type sont autorisées à partir du moment où elles respectent la cardinalité. Pour qu'un MultiValDT δtmv2 ayant une cardinalité C2 soit sous type d'un MultiValDT δtmv1 ayant une cardinalité C1 il faut que l'intervalle d'entiers défini par C2 soit inclus dans l'intervalle d'entiers défini par C1. En effet, si la cardinalité est [1..8] pour C1 et [2..5] pour C2, les valeurs de δtmv2 seront correctes pour δtmv1.
Le super δ-type commun à deux MultiValDT non reliés par sous-typage, est un MultiValDT définissant une cardinalité ayant pour minimum le plus petit minimum des deux δ-types et pour maximum le plus grand maximum des deux δ-types. Si l'on considère un δ-type avec une cardinalité C1 de [1..8] et un δ-type avec une cardinalité C2 de [10..100], le super δ-type commun définira une cardinalité C3 de [1..100].
Le dernier cas à considérer est le cas où il faut classer un MultiValDT δtmv1 définissant un domaine S1 et un MultiValDT δtmv2 définissant une cardinalité C2. Les règles suivantes s'appliquent alors :
S1 = X (X={x1,...,xn}) δtmv1 < δtmv2 ssi ∀ x ∈ X, length x ∈ C2S1 = !X (X={x1,...,xn}) Impossible de classer les deux types puisque l'ensemble de toutes les valeurs du C-type est infini.
Les RecordDT restreignent les RecordCT en définissent pour domaines des ensembles de valeurs autorisées ou interdites. On retrouve donc la même définition que celles des MultiValDT. Par conséquent, les règles citées pour les MultiValDT s'appliquent. Tout comme pour les MultiValDT, les points iii et iv de ces règles sont particulièrement difficile à satisfaire car il suffit qu'un des δ-types associés aux étiquettes soit infini pour que l'ensemble des valeurs du C-type de base soit infini. De plus, même lorsque cet ensemble n'est pas infini, le nombre de valeurs possible peut être astronomique.
De la même façon, pour ce qui est de déterminer un super δ-type commun à deux RecordDT, les règles définies pour MultiValDT s'appliquent.
Actuellement, il n'est pas possible de définir un δ-type à partir d'un RecordCT ou d'un MultiValCT en redéfinissant les δ-types des éléments des collections ou étiquettes. Cette possiblité pourrait nécessité des corrections sur la définitions des relations de sous-typage.