

Voilà quelques années, un de mes amis passait sa lune de miel dans un coin perdu d'Irlande. Sa femme et lui marchaient sur une plage déserte lorsqu'ils virent s'approcher deux personnes... qui n'étaient autres que le patron de mon ami et sa femme. Aucun des couples n'avait eu vent des projets de l'autre : leur rencontre était une pure coïncidence.
Si nous sommes si fascinés par les coïncidences, c'est parce que nous avons une piètre intuition des probabilités qui s'y rapportent. Examinons l'une des coïncidences les plus communes : celle des dates d'anniversaire. Combien de personnes doit-on réunir dans une pièce pour avoir une probabilité supérieure à un demi que deux d'entre elles au moins aient la même date de naissance ? Pour simplifier, supposons qu'il n'y a pas d'années bissextiles, de sorte qu'il n'y ait que 365 dates d'anniversaire possibles. Supposons également chaque date équiprobable , ce qui n'est pas tout à fait exact : il naît plus d'enfants à certaines époques de l'année qu'à d'autres (on pourrait tenir compte de ces facteurs, mais cela compliquerait le calcul sans modifier les conclusions).
Alors, combien de personnes faut-il dans la pièce ? Cent ? Deux cents ? Mille ? Lorsque des chercheurs posèrent cette question à des étudiants d'Université, la moyenne de leurs estimations fut 385. Valeur excessive à l'évidence, puisque, dès qu'il y a 366 personnes, une coïncidence au moins est garantie d'après le principe des tiroirs (le même, qui stipule que si l'on place trois chemises dans les tiroirs d'un meuble à deux tiroirs, un des tiroirs contient nécessairement plus d'une chemise ; ici les dates sont l'équivalent des tiroirs, et les personnes correspondent aux chemises). En fait, la réponse correcte est bien inférieure : seulement 23 personnes.
Pour ce calcul, il est plus aisé de déterminer la probabilité qu'un événement ne se produise pas. En soustrayant ce nombre à un, on obtient la probabilité que l'événement se produise. Par exemple, quand l'événement «Deux personnes au moins ont la même date d'anniversaire» n'est-il pas réalisé ? Lorsque toutes les dates sont différentes. Supposons qu'il y ait d'abord une personne dans la pièce et introduisons les autres personnes une à une. Nous pouvons calculer la probabilité qu'une nouvelle personne ait une date d'anniversaire différente de toutes celles des personnes déjà entrées. Ces probabilités décroissent constamment, et celles d'une coïncidence croissent en conséquence. Or, un événement est plus vraisemblable que son contraire si et seulement si sa probabilité est supérieure à 1/2. Dès que la probabilité de dates toutes différentes devient inférieure à 1/2, nous savons que l'existence d'une coïncidence au moins est plus probable que son contraire.
Avec une seule personne, que nous nommerons Arthur, pas de coïncidence possible : la probabilité cherchée est donc égale à un. Voici qu'entre Élise. Son anniversaire peut être l'un des 365 jours de l'année, mais, comme Arthur est né l'un de ces jours, la probabilité d'avoir des dates distinctes est égale à 364/365 (le quotient du nombre de cas favorables et du nombre de cas possibles). Puis arrive Pierre. Il reste 363 dates non prises, d'où la probabilité d'avoir une date distincte des deux autres, qui est de 363/365. La probabilité combinée d'avoir trois dates distinctes est égale au produit (364/365) x (363/365) (de la même façon que la probabilité d'obtenir deux face de suite, à pile ou face, est égale à 1/2 x 1/2).
Nous voyons apparaître la formule générale. Lorsque Catherine entre dans la pièce, la probabilité d'avoir quatre dates distinctes est égale à :
(364/365) x (363/365) x (362/365).
Plus généralement, lorsqu'il y a n personnes dans la pièce, la probabilité d'avoir n dates différentes est :
(364/365) x (363/365) x ... x ((365 - n + 1)/365)).
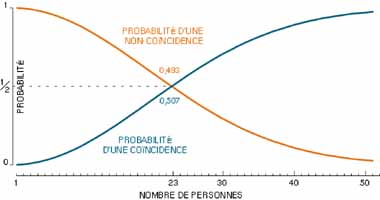
Il nous suffit donc de calculer les valeurs successives de cette expression pour savoir à partir de quel n elle devient inférieure à 1/2. Vingt-deux personnes ont une probabilité de 0,524 d'avoir des dates de naissance toutes distinctes, et ce résultat descend à 0,493 pour 23 personnes. Donc, dès que 23 personnes sont rassemblées, la probabilité d'une coïncidence au moins est 1 - 0,493, soit 0,507 : l'événement est légèrement plus probable que son contraire.
Testez ce résultat dans des rassemblements de plus de 23 personnes en prenant des paris : à la longue, vous gagnerez. Plus il y aura de monde, plus vite vous gagnerez. La plupart des participants jugeront qu'une coïncidence est improbable, parce qu'ils se focaliseront sur un aspect trompeur du problème : le nombre de personnes dans la pièce. Bien que 23 soit petit, il existe pour 23 personnes, 253 manières de les associer par paires (pour n, il y en a n(n - 1)/2). Ce grand nombre est révélateur de la probabilité d'une coïncidence.
Robert Matthews, un journaliste britannique et mathématicien, et Fiona Stones ont vérifié ce résultat d'une manière expérimentale. Dans un match de football, il y a 23 personnes sur le terrain : les deux équipes de 11 joueurs et l'arbitre. Donc, l'événement «deux joueurs au moins ont la même date d'anniversaire» est plus probable que son contraire. Ils se sont intéressés aux matchs de première division du Royaume-Uni joués le 19 avril 1997. Sur dix rencontres, six étaient avec coïncidences, et quatre sans.
En fait, dans deux des matchs, il y avait deux coïncidences ! Dans celui opposant Liverpool à Manchester United, deux joueurs étaient nés le 21 janvier et deux le 1er août ; entre Chelsea et Leicester City les coïncidences étaient le 1er novembre et le 22 décembre. Cette double coïncidence est également prédite par la théorie des probabilités. Elle évalue la probabilité d'avoir deux coïncidences parmi 23 personnes à 0,111... : l'événement se produit donc en moyenne tous les neuf matchs de football. La probabilité d'avoir trois coïncidences parmi 23 personnes est égale à 0,018..., et celle d'avoir une coïncidence triple (trois personnes parmi les 23 ont la même date de naissance) est égale à 0,007... : on l'observe une fois sur 143 rencontres en moyenne. Amusez-vous à vérifier ces valeurs avec les matchs de la Coupe du monde.
Intuition, intuition...
Une question légèrement différente à présent : combien de personnes en plus de vous-même doivent être dans la pièce pour que l'événement «une personne au moins a votre date de naissance» soit plus probable que son contraire ? On pourrait croire que la réponse est (364/2) + 1, soit 183, puisqu'il y a 364 dates différentes de la vôtre et que, si plus de la moitié de ce nombre de personnes se trouve dans la salle, vous avez plus d'une chance sur deux de partager votre date de naissance avec l'une d'elles. Mais la réponse correcte est 253.
Pour obtenir ce nombre, reprenons la technique déjà utilisée : on cherche la probabilité que les dates d'anniversaire soient différentes de la vôtre, puis l'on soustrait ce nombre à un. Vous êtes déjà dans la pièce et les autres personnes se présentent l'une après l'autre : Arthur, Élise, Pierre, Catherine, etc. La probabilité qu'Arthur ait une date de naissance différente de la vôtre est 364/365. La probabilité qu'Élise ait une date de naissance différente de la vôtre est encore 364/365. Il en est de même pour tous les autres. Nous nous désintéressons ici des coïncidences entre dates de naissance de personnes autres que vous, par exemple si Arthur et Élise sont nés le 3 avril. Seul compte si une date de naissance est la même que la vôtre, de sorte que, après l'entrée de n personnes, la probabilité pour qu'elles aient toutes des dates différentes de la vôtre est égale à (364/365)n. La première valeur de n pour laquelle cette expression est inférieure à 1/2 est 253 ((364/365)253 = 0,499...).
Incidemment, le fait que cette réponse soit égale au nombre de paires dans le premier problème (avec 23 personnes) semble n'avoir aucune signification mathématique. Une coïncidence donc !
Que nous enseignent ces calculs de probabilité ? D'abord ils nous engagent à ne pas être impressionné outre mesure par des événements qui semblent improbables : ils ne le sont peut-être pas. Une paire de footballeurs ayant la même date d'anniversaire seront probablement surpris de la coïncidence, mais tout match a plus d'une chance sur deux d'en posséder une. Les joueurs se souviendront probablement de cette coïncidence pendant des années, mais les 252 autres paires de joueurs ne s'étonneront pas que leurs dates de naissance ne coïncident pas, car nous remarquons les coïncidences et ignorons les non-coïncidences, et faisons de la sorte paraître les premières plus importantes qu'elles ne le sont en réalité.
La rencontre de mon ami durant sa lune de miel paraît moins surprenante
si l'on songe au nombre de couples qu'il a rencontrés durant sa vie
et qui n'étaient pas son patron et son épouse.

Bibliographie :

N° 249 juillet 1998
© Pour la Science (1998)
Cet article est reproduit dans SMEL grâce à l'aimable autorisation de Ian Stewart
qui en possède les droits de reproduction électronique.