En pratique, l'ensemble des valeurs que peut prendre ![]() est
est
![]() ou une
partie de
ou une
partie de
![]() .
.
Déterminer la loi d'une variable aléatoire discrète c'est
Point de vue fréquentiste. Rappelons que le seul sens pratique que l'on puisse donner à la notion de probabilité est celui d'une limite de fréquences expérimentales. C'est aussi le sens qu'il faut donner à la notion de loi discrète.
Répétons ![]() fois indépendamment l'expérience
aléatoire
à l'issue
de laquelle
fois indépendamment l'expérience
aléatoire
à l'issue
de laquelle ![]() est mesurée. On obtient ainsi un
est mesurée. On obtient ainsi un ![]() -uplet
-uplet
![]() de
variables aléatoires indépendantes
de même loi
que
de
variables aléatoires indépendantes
de même loi
que ![]() (cela s'appelle un
échantillon).
On peut sur ce
(cela s'appelle un
échantillon).
On peut sur ce ![]() -uplet
calculer les
fréquences expérimentales
des évènements "
-uplet
calculer les
fréquences expérimentales
des évènements "![]() ".
".
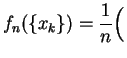 1
1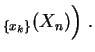
D'après la
loi des grands nombres
cette
fréquence
doit converger vers
![]() . Pour tout
. Pour tout ![]() les
fréquences expérimentales
les
fréquences expérimentales
![]() définissent une
loi de probabilité discrète
sur l'ensemble des
définissent une
loi de probabilité discrète
sur l'ensemble des
![]() .
.
On représente graphiquement une
loi discrète
par un
diagramme en bâtons
: il consiste à tracer au dessus de l'abscisse ![]() un segment
vertical de longueur proportionnelle à
un segment
vertical de longueur proportionnelle à ![]() .
.
Les lois discrètes les plus courantes sont les suivantes.
Loi uniforme.
La
loi uniforme
sur un ensemble fini est la loi des "tirages au hasard"
dans cet ensemble, ou équiprobabilité. Elle donne la même
probabilité
![]() à tous les éléments de l'ensemble, s'il est
de cardinal
à tous les éléments de l'ensemble, s'il est
de cardinal ![]() .
.
Loi de Bernoulli.
Les plus simples des
variables aléatoires
discrètes sont les indicatrices
d'évènements. Si ![]() est un évènement de
probabilité
est un évènement de
probabilité
![]() , la variable aléatoire
1
, la variable aléatoire
1![]() prend la valeur 1 si
prend la valeur 1 si ![]() est réalisé, et 0 sinon.
Sa loi est la
loi de Bernoulli
de paramètre
est réalisé, et 0 sinon.
Sa loi est la
loi de Bernoulli
de paramètre ![]() .
.
Les deux autres exemples de base sont la loi binomiale et la loi géométrique.
Loi binomiale.
On répète la même expérience ![]() fois indépendamment et on compte
le nombre de fois où l'évènement
fois indépendamment et on compte
le nombre de fois où l'évènement ![]() se produit. On considèrera la
répétition des
se produit. On considèrera la
répétition des ![]() expériences comme une nouvelle expérience globale.
Comme seul l'évènement
expériences comme une nouvelle expérience globale.
Comme seul l'évènement ![]() nous importe, on pourra ne retenir de
l'expérience globale qu'un
nous importe, on pourra ne retenir de
l'expérience globale qu'un ![]() -uplet de booléens du type :
-uplet de booléens du type :
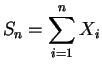 le nombre de fois où
le nombre de fois où 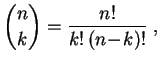
![$\displaystyle P[S_n=k]=\binom{n}{k}p^k(1-p)^{n-k}\;,\quad\forall k=0,\ldots,n\;.
$](img285.gif)
A retenir :
Le nombre d'occurrences d'un même évènement au cours de ![]() expériences
indépendantes
suit une
loi binomiale.
expériences
indépendantes
suit une
loi binomiale.
Simulation
:
En sortie de l'algorithme suivant, ![]() suit la
loi binomiale
suit la
loi binomiale
![]() .
C'est la situation typique où on rencontre la
loi binomiale,
mais ce n'est pas la méthode de
simulation
la plus efficace.
.
C'est la situation typique où on rencontre la
loi binomiale,
mais ce n'est pas la méthode de
simulation
la plus efficace.
![]()
Répéter ![]() fois
fois
Si ( Random
![]() ) alors
) alors
![]()
finSi
finRépéter
Remarque : C'est une bonne habitude à prendre que de vérifier
que la somme des
probabilités
calculées vaut 1. Ici :
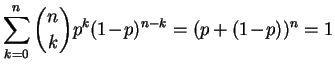 ,
par la formule du binôme de Newton (d'où le nom de loi binomiale).
,
par la formule du binôme de Newton (d'où le nom de loi binomiale).
Loi géométrique.
Le problème ici est d'observer une suite de répétitions
indépendantes
d'une même expérience. On s'intéresse au moment où l'évènement
![]() se produit pour la première fois. On suppose que la
probabilité
se produit pour la première fois. On suppose que la
probabilité
![]() de
de ![]() est strictement positive.
est strictement positive.
Notons ![]() le rang de l'expérience au cours de laquelle
le rang de l'expérience au cours de laquelle ![]() se produit pour
la première fois. C'est une
variable aléatoire,
qui
dépend de l'expérience
aléatoire
:
se produit pour
la première fois. C'est une
variable aléatoire,
qui
dépend de l'expérience
aléatoire
:
L'ensemble des valeurs possibles pour ![]() est
est
![]() .
Pour tout
.
Pour tout ![]() on a :
on a :
![$\displaystyle P[N=k]=P[(\underbrace{\overline A\ldots\overline A}_{k-1}A)]
=\underbrace{(1\!-\!p) \cdots (1\!-\!p)}_{k-1} p=p\; (1\!-\!p)^{k-1}\;.
$](img296.gif)
A retenir : Le nombre d'expériences indépendantes nécessaires à la première observation d'un évènement suit une loi géométrique.
Simulation
:
En sortie de l'algorithme suivant, ![]() suit la
loi géométrique
suit la
loi géométrique
![]() . C'est la situation typique où on
rencontre la
loi géométrique,
mais ce n'est pas la méthode de
simulation
la plus efficace.
. C'est la situation typique où on
rencontre la
loi géométrique,
mais ce n'est pas la méthode de
simulation
la plus efficace.
![]()
Répéter
![]()
Jusqu'à (
Random
![]() )
)
Remarque :
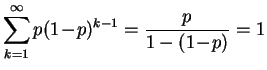 .
.
La conséquence de cette remarque est la suivante : au cours d'une suite
d'expériences
indépendantes,
tout évènement finira par se produire si
sa
probabilité
est strictement positive. Une
suite aléatoire
de 0 et de 1 doit
nécessairement contenir ![]() zéros à la suite. Si un singe tape au
hasard sur une machine à écrire, il finira forcément par taper Les
Misérables sans fautes, de la première majuscule au dernier point.
zéros à la suite. Si un singe tape au
hasard sur une machine à écrire, il finira forcément par taper Les
Misérables sans fautes, de la première majuscule au dernier point.
Pour comprendre ce paradoxe, calculons la
probabilité
qu'un évènement
de
probabilité
![]() se produise au plus tard à la
se produise au plus tard à la ![]() -ème expérience.
-ème expérience.
![$\displaystyle P[N\leq k]
=\sum\limits_{i=1}^kp(1\!-\!p)^{i-1}
=p\frac{1-(1\!-\!p)^{k}}{1-(1\!-\!p)}=1-(1\!-\!p)^k\;.
$](img302.gif)
Même si toutes les particules de l'univers étaient des singes tapant à raison de 10 caractères par seconde, il faudrait beaucoup plus de temps qu'il ne s'en est écoulé depuis le début de l'univers pour avoir une chance non négligeable d'en voir un taper Les Misérables.
La
loi binomiale
et la
loi géométrique
apparaissent fréquemment
dans l'analyse des algorithmes de
simulation.
Voici l'exemple du calcul
d'une
probabilité conditionnelle.
La programmation
directe de la définition intuitive (proportion de fois où ![]() est
réalisé parmi celles où
est
réalisé parmi celles où ![]() l'est aussi) conduirait à l'algorithme
suivant.
l'est aussi) conduirait à l'algorithme
suivant.
![]()
![]()
Répéter ![]() fois
fois
expérience
Si ![]() réalisé alors
réalisé alors
![]()
Si ![]() réalisé alors
réalisé alors
![]()
finSi
finSi
finRépéter
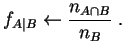
Rien n'empêche ![]() d'être nul à l'issue de
d'être nul à l'issue de ![]() expériences (même
si c'est peu probable). On préfère fixer
expériences (même
si c'est peu probable). On préfère fixer ![]() et écrire :
et écrire :
Répéter ![]() fois
fois
Répéter
expérience
Jusqu'à ![]() réalisé
réalisé
Si ![]() réalisé alors
réalisé alors
![]()
finSi
finRépéter
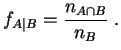
Exécuter cet algorithme revient à calculer la
fréquence expérimentale
de ![]() à l'issue de
à l'issue de ![]() répétitions
indépendantes
d'une
expérience globale. Cette expérience globale consiste à répéter
indépendamment une même expérience jusqu'à la première réalisation
de
répétitions
indépendantes
d'une
expérience globale. Cette expérience globale consiste à répéter
indépendamment une même expérience jusqu'à la première réalisation
de ![]() . Notons
. Notons ![]() la
probabilité
relative à la "petite" expérience,
et
la
probabilité
relative à la "petite" expérience,
et ![]() la
probabilité
relative à l'expérience globale. La
"durée" de cette expérience globale est un nombre entier
aléatoire.
Il suit la
loi géométrique
de paramètre
la
probabilité
relative à l'expérience globale. La
"durée" de cette expérience globale est un nombre entier
aléatoire.
Il suit la
loi géométrique
de paramètre ![]() .
On démontre que la variable
.
On démontre que la variable
![]() suit la
loi binomiale
de
paramètres
suit la
loi binomiale
de
paramètres ![]() et
et ![]() .
.
Exemple :
![]()
Répéter ![]() fois
fois
Répéter
![]() Random
Random
![]() (* lancer d'un dé *)
(* lancer d'un dé *)
Jusqu'à (![]() pair)
(*
pair)
(* ![]() est l'évènement "
est l'évènement "![]() pair" *)
pair" *)
Si ![]() alors
alors
![]() (*
(* ![]() est l'évènement "
est l'évènement "![]() " *)
" *)
finSi
finRépéter
![]()
En sortie de cet algorithme,
![]() contient un nombre d'autant plus proche de
contient un nombre d'autant plus proche de ![]() que
que ![]() est grand.
Le nombre de répétitions de l'expérience au cours de chaque passage
dans la boucle principale suit la
loi géométrique
est grand.
Le nombre de répétitions de l'expérience au cours de chaque passage
dans la boucle principale suit la
loi géométrique
![]() .
.
D'autres lois discrètes classiques sont souvent utilisées. Il s'agit des lois de Poisson, des lois hypergéométriques et des lois binomiales négatives.
Loi de Poisson. De nombreuses variables aléatoires discrètes correspondent à des comptages d'objets possédant un caractère relativement rare dans un grand ensemble : atomes d'un isotope, molécules d'un élément chimique, bactéries, virus, individus porteurs d'un gène particuler,... On utilise souvent une loi de Poisson comme modèle pour ces comptages.
Une
variable aléatoire
suit la
loi de Poisson
de paramètre ![]() si
elle prend ses valeurs dans
si
elle prend ses valeurs dans
![]() , et si pour tout
, et si pour tout
![]() ,
,
![$\displaystyle P[X=k]=e^{-\lambda }\frac{\lambda^k}{k!}\;.
$](img323.gif)
Loi hypergéométrique.
La
loi hypergéométrique
est la loi des "tirages sans remise". D'une
population
de taille ![]() , on extrait
au hasard
un échantillon
(sous-ensemble) de taille
, on extrait
au hasard
un échantillon
(sous-ensemble) de taille ![]() . Parmi les
. Parmi les ![]() individus,
individus, ![]() sont "marqués". Le nombre
sont "marqués". Le nombre ![]() d'individus marqués sur les
d'individus marqués sur les ![]() individus
choisis suit la
loi hypergéométrique
de paramètres
individus
choisis suit la
loi hypergéométrique
de paramètres ![]() ,
, ![]() et
et ![]() ,
La
variable aléatoire
,
La
variable aléatoire
![]() prend ses valeurs dans l'ensemble
prend ses valeurs dans l'ensemble
![]() ,
et pour tout
,
et pour tout
![]() :
:
![$\displaystyle P[X=k]=\frac{\binom{m}{k}\,\binom{N-m}{n-k} }{\binom{N}{n}}\;.
$](img326.gif)
On rencontre fréquemment cette loi dans les jeux de hasard.
Loi binomiale négative.
Cette loi est souvent utilisée dans les comptages en biologie. Le modèle
de base qui la définit peut encore s'écrire en termes d'indicatrices
d'évènements indépendants,
comme pour les
lois binomiales
et
géométriques.
Au cours d'une suite d'expériences
aléatoires
indépendantes,
observons un évènement ![]() de
probabilité
de
probabilité
![]() . Notons
. Notons
![]() le nombre d'observations de
le nombre d'observations de
![]() avant la
avant la ![]() -ième
observation de
-ième
observation de ![]() . Alors
. Alors ![]() suit la
loi binomiale négative
de paramètres
suit la
loi binomiale négative
de paramètres
![]() et
et ![]() , notée
, notée
![]() . L'ensemble des valeurs prises est
. L'ensemble des valeurs prises est
![]() et
pour tout
et
pour tout
![]() ,
,
![$\displaystyle P[X=k] = \binom{n+k-1}{n-1} p^n (1-p)^k\;.
$](img331.gif)
![]()
Répéter ![]() fois
fois
Tantque
(Random
![]() )
)
![]()
finTantque
finRépéter