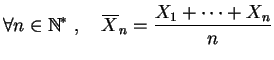 et
et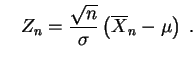
![$\displaystyle \lim_{n\rightarrow\infty}\,P[a<Z_n<b]\;=\;
\int_a^b \frac{1}{\sqrt{2\pi}}e^{-x^2/2}\,dx
\;.
$](img592.gif)
En simulation, la situation typique est celle où on exécute un très grand nombre de fois une boucle, en calculant à chaque passage des réalisations de variables aléatoires indépendantes. Le résultat attendu est en général l'estimation d'une espérance. Pas plus en simulation qu'en physique ou en biologie on ne donnera un résultat sans indication sur sa précision. C'est le théorème central limite qui permet de calculer cette précision.
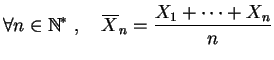 et
et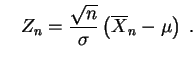
![$\displaystyle \lim_{n\rightarrow\infty}\,P[a<Z_n<b]\;=\;
\int_a^b \frac{1}{\sqrt{2\pi}}e^{-x^2/2}\,dx
\;.
$](img592.gif)
Interprétation.
Dans le
théorème central limite,
![]() est la valeur
à estimer. Les
est la valeur
à estimer. Les ![]() valeurs
valeurs
![]() constituent un
échantillon
de mesures
aléatoires
indépendantes
d'espérance
constituent un
échantillon
de mesures
aléatoires
indépendantes
d'espérance
![]() . La quantité
. La quantité
![]() est la
moyenne empirique
de
l'échantillon,
qui
d'après la
loi des grands nombres
doit converger vers
l'espérance
est la
moyenne empirique
de
l'échantillon,
qui
d'après la
loi des grands nombres
doit converger vers
l'espérance
![]() .
Le
théorème central limite
donne la précision de cette approximation.
On peut le lire intuitivement comme suit. Si
.
Le
théorème central limite
donne la précision de cette approximation.
On peut le lire intuitivement comme suit. Si ![]() est assez grand alors
est assez grand alors ![]() est très probablement compris entre
est très probablement compris entre ![]() et
et ![]() (la probabilité
est
(la probabilité
est ![]() ). Soit encore :
). Soit encore :
![$\displaystyle \frac{X_1+\cdots +X_n}{n} - \mu\;\in\;
\left[-\frac{3\sigma}{\sqrt n}\;;\;
+\frac{3\sigma}{\sqrt n}\right]
\;,
$](img595.gif)
Le
théorème central limite
est utilisé pour des valeurs
finies de ![]() .
L'idée concrète est la suivante. Si
.
L'idée concrète est la suivante. Si ![]() est assez grand, la variable
centrée réduite
(espérance 0,
variance
1)
est assez grand, la variable
centrée réduite
(espérance 0,
variance
1) ![]() associée à la
somme de
associée à la
somme de ![]() variables indépendantes
suit
approximativement la loi
variables indépendantes
suit
approximativement la loi
![]() . Si on réalise
suffisamment de
simulations
de
. Si on réalise
suffisamment de
simulations
de ![]() et si on trace un
histogramme
des
valeurs obtenues, celui-ci ne sera pas très loin de la courbe
et si on trace un
histogramme
des
valeurs obtenues, celui-ci ne sera pas très loin de la courbe
![]() . Pas plus loin en tout
cas que si on avait simulé des
variables aléatoires
de loi
. Pas plus loin en tout
cas que si on avait simulé des
variables aléatoires
de loi
![]() . Si
. Si ![]() suit la loi
suit la loi
![]() , alors
, alors
![]() suit la loi
suit la loi
![]() . On peut aussi dire que
pour n assez grand une somme de n
variables aléatoires indépendantes
indépendantes
suit approximativement une
loi normale, dont
l'espérance
et la
variance
sont respectivement la somme des espérances et la somme des
variances
des variables que l'on ajoute.
Le problème est de savoir à partir de quelle valeur
. On peut aussi dire que
pour n assez grand une somme de n
variables aléatoires indépendantes
indépendantes
suit approximativement une
loi normale, dont
l'espérance
et la
variance
sont respectivement la somme des espérances et la somme des
variances
des variables que l'on ajoute.
Le problème est de savoir à partir de quelle valeur ![]() est "assez grand", pour la précision désirée.
Cela dépend beaucoup de la loi des
est "assez grand", pour la précision désirée.
Cela dépend beaucoup de la loi des ![]() . L'approximation
est d'autant meilleure que la loi des
. L'approximation
est d'autant meilleure que la loi des ![]() est plus symétrique.
En particulier, le bon comportement de la
loi uniforme
vis à vis du
théorème central limite
conduit à un algorithme approché de
simulation
pour la loi
est plus symétrique.
En particulier, le bon comportement de la
loi uniforme
vis à vis du
théorème central limite
conduit à un algorithme approché de
simulation
pour la loi
![]() .
.
![]()
Répéter ![]() fois
fois
![]() Random
Random
finRépéter
Justification :
Si ![]() désigne la suite des appels de
Random
(suite de variables
indépendantes
de
loi uniforme
sur
désigne la suite des appels de
Random
(suite de variables
indépendantes
de
loi uniforme
sur ![]() , on a :
, on a :
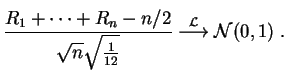
On évite une division et on obtient une approximation déjà correcte en
prenant ![]() . Cet algorithme n'est cependant pas conseillé avec les
générateurs classiques. Son principal
inconvénient est de consommer trop d'appels de
Random,
ce qui pose le
problème de la dépendance des réalisations successives.
. Cet algorithme n'est cependant pas conseillé avec les
générateurs classiques. Son principal
inconvénient est de consommer trop d'appels de
Random,
ce qui pose le
problème de la dépendance des réalisations successives.
Pour des lois plus dissymétriques comme la loi exponentielle, l'approximation normale n'est pas valable pour des sommes de quelques dizaines de variables. On peut la considérer comme justifiée à partir de quelques centaines. En simulation, ce sont des milliers, voire des millions de variables qui sont engendrées, et l'approximation normale est tout à fait légitime.