Dernière modification : 16 février 1999, Philippe Genoud

Le thème de cette semaine consiste à réaliser des actions récursives (thème actuel du cours et des TD d'algorithmique). Plus précisément il s'agit d'écrire les programmes JAVA correspondant aux exercices de tracés de figures géométrique proposés dans le chapitre 8 (Actions récursives) du cours d'algorithmique de Pierre-Claude Scholl.

Bien que ce thème relève plus du cours d'algorithmique que du cours de programmation orientée objet, nous allons en profiter pour expérimenter avec les packages.

Pour réaliser ces exercices vous disposez de trois classes définies dans un package de nom pg.coursjava.logo. Ce package comme son nom l'indique permet de faire en JAVA du dessin à la "Logo". Logo est un langage destiné à apprendre de manière ludique la programmation. Pour cela le langage Logo permet de manipuler une "tortue" qui est très similaire à  la plume de la machine de tracés définie dans le cours d'algorithmique.

Ce package regroupe trois classes :

- une classe Pt qui permet de définir des points.
- une classe Fenetre qui permet de gérer la fenêtre de tracé.
- une classe Plume qui permet de gérer la plume dans la fenêtre de tracé.

Si vous voulez consulter les sources de ces classes : Pt.java, Fenetre.java, Plume.java

Pour réaliser ce Tp deux solutions sont envisageables :

- écrire un programme (une classe) ne comportant que des méthodes statiques : Carres.java
- étendre la classe Plume (par héritage) en lui ajoutant des méthodes de tracé de plus haut niveau (qui bien sûr peuvent être récursives) : Carres2.java

Lisez ces programmes et adoptez la stratégie qui vous convient le mieux. Personnellement je préfère la deuxième qui relève plus d'une approche orientée objet.

Bien sûr pour pouvoir compiler ces classes il faut que vous indiquiez dans votre classpath le chemin d'accès aux classes du package pg.coursjava.logo.

Deux solution se présentent :

a) Recompiler le package pg.coursjava.logo

1. créez chez vous une hiérarchie de répertoires sources/pg/coursjava/logo et recopier dans le répertoire logo les fichier sources des différentes classes du package.
2. créez chez vous un répertoire classes qui vous servira à ranger vos .class et les packages que vous écrirez ou que vous ramènerez .
3. placez vous dans le répertoire sources
4. compilez les classes du package pg.coursjava.logo par la commande

javac "-d ..../classes" pg/coursjava/logo/Fenetre.java
qui a pour effet de placer les fichiers .class dans le répertoire indiqué par l'option -d et où ..../classes est le chemin d'accès à la racine des répertoires correspondants aux packages. (vous constaterez qu'une hierarchie de répertoires respectant le nom du package a été créée dans le répertoire classes)
5. par la suite il faudra indiquer comme classpath lorsque vous compilerez vos nouveaux programmes :

.   le répertoire courant
..../classes  le chemin d'accès à la racine des répertoires correspondants aux packages.

1. recopiez chez vous le fichier logo.jar(en cliquant sur le bouton droit de la souris et en sélectionnant l'item enregistrer le lien sous du menu qui apparait alors. Si vous le souhaitez vous pourrez faire la commande jar -tvf logo.jar pour voir son contenu).
2. n'oubliez pas ensuite d'intégrer ce fichier jar à votre classpath pour compiler vos classes utilisant les classes de ce package (vous vous reporterez pour cela au Tp visages1).

1) après avoir installé le package, compiler et exécuter les programmes exemples Carre.java et Carre2.java.

2) écrire les actions récursives correspondant aux exercices du cours d'algorithmique dont vous trouverez dans ce qui suit une version html.
(le cours et les images ont été scannés d'où une mauvaise qualité des images et peut être encore quelques erreurs dues à la mauvaise précision du programme d'OCR ... et à ma fatigue pour relire tout cela).

Tracé de carrés emboîtés

Contexte : une machine de tracés

(Cf. [SP88], pp38, 39)

Nous définissons une machine-tracés, c'est-à-dire un répertoire de primitives élémentaires de tracés. Nous l'utilisons pour illustrer la notion d'action, le raisonnement sur les états et les diverses formes de composition d'actions.

description de l'état de lamachine

L'état de la machine-tracés est caractérisé par l'état de deux composants : l'écran et la plume de tracé. L'écran est un ensemble de points qui peuvent être éteints ou allumés. Une figure est matérialisée par des points allumés. Les points sont désignés à l'aide de coordonnées définies dans un système d'axes Ox, Oy dont l'origine, nommée centre (de l'écran) appartient au lexique de la machine-tracés. Un état de l'écran, c'est-à-dire son état à un instant donné, est caractérisé par les figures qu'il comporte. L'état particulier dans lequel tous les points sont éteints est nommé écran vide. Lorsque nous voulons indiquer qu'aucune contrainte particulière n'est imposée à l'écran, nous disons qu'il est dans un état indifférent.

La machine-tracés manipule une plume dont l'état est défini par trois attributs :

• Une position d'écriture, en abrégé pe : elle peut être basse ou haute.
• Une position dans le plan, en abrégé pp : c'est un point du plan. Le cas échéant, nous ledécrivons par un couple de coordonnées.
• Un cap : c'est le sens de la plume, défini par un angle par rapport à l'axe Ox, orienté dans le sens trigonométrique. Cet angle est donné en degrés.

Les primitives du répertoire sont regroupées selon le type de modifications qu'elles apportent à l'état de l'écran ou de la plume.

modification globale de l'écran etdela plume
 

• Vider vide l'écran et place la plume au centre, en position haute, cap Ouest-Est.
• Effacer vide l'écran sans modifier l'état de la plume.

• Lever et Baisser mettent la plume en position "haute" ou "basse"

• Avancer et Reculer, en abrégé Av et Re, font avancer ou reculer la plume d'une distance donnée, selon le cap de la plume. La distance est donnée sous forme d'un nombre entier ou réel, par exemple Av (50) ou Re (30.5). Notons que Av (-50) est équivalent à Re (50). L'interprétation exacte de l'unité de mesure dépend des caractéristiques physiques de l'environnement dans lequel la machine sera réalisée.
• Placer, en abrégé Plc, permet de mettre la plume en un point du plan donné. Le point est donné sous forme d'un couple de coordonnées, par exemple Plc (-10, 35.3).

modification du cap de la plume

• TournerGauche et TournerDroite, en abrégé TrG et TrD, changent le cap selon une valeur d'angle donnée en degrés. Par exemple, TrG (35) augmente modulo 360 le cap de la plume de 35 degrés. TrD (45) le diminue modulo 360 de 45 degrés. TrG (35) a le même effet que TrD (325).
• Orienter, en abrégé Ort, donne à la plume le cap donné en degrés. Par exemple, Ort (90) donne à la plume le cap SudNord.

Définir une action de tracé permettant de tracer une figure formée de n carrés emboités (n=4 sur la figure 8. 1). La figure doit être tracée sans lever la plume et sans tracer deux fois le même trait. On peut toutefois passer plusieurs fois par le même point.

Figure 8.1: 4 carrés emboîtés à tracer sans lever la plume

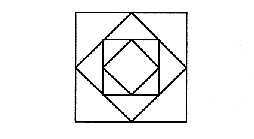
Une telle figure est définie par le nombre de carrés emboîtés et son carré extérieur. On convient ici qu'un carré est défini par son sommet, sa taille et son cap : le sommet du carré est l'un de ses sommets ; la taille du carré est la taille de ses côtés ; le cap du carré est le cap du côté passant par le sommet tel qu'un observateur placé sur ce sommet et regardant dans le sens de ce côté, voit tous les autres côtés à sa gauche et devant lui .

Ainsi une figure est donnée par son ordre (nombre de carrés emboîtés), son sommet (sommet du carré extérieur), sa taille (taille du carré extérieur) et son cap (cap du carré extérieur).

On spécifie l'action Tcaremb, de tracé de carrés emboîtés :

• Base: la figure d'ordre 1 comporte un seul carré ;
• Construction récurrente : une figure d'ordre n+l est composée d'un carré extérieur contenant une figure d'ordre n, comme l'illustre la figure 8.2.

Figure 8.2: Une figure d'ordre n +1 est constituée d'un carré et d'une figure d'ordre n.

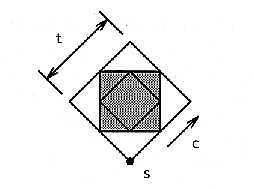
Pour tenir compte de la contrainte de tracé, on décompose le carré extérieur en deux parties délimitées par l'un des points communs au carré extérieur et à la figure intérieure. On décompose ainsi le tracé d'un carré en deux actions intermédiaires de tracé : TDébutCar et TFinCarde telle sorte que

Tdébutcar (t) : Av (t/2)

Tfincar (t) :

Av (t/2) ; TrG (90)
i parcourant [1...3] : Av (t) ; TrG (90)

Tcaremb (n, t)
{ plume basse au sommet et au cap de la figure }

si n 1 alors

Dessins récursifs

Observer l'exécution de l'action récursive Tcaremb de tracé de carrés emboités :

Donner la trace de l'exécution de l'algorithme Vider ; Baisser ; Tcaremb (4, 4) sous forme de la liste des appels engendrés, mise en page avec une indentation reflétant la structure emboîtée des appels récursifs (Cf. 8.A.a).

• Spécifier une action qui produit cette trace, puis la réaliser sous forme récursive.

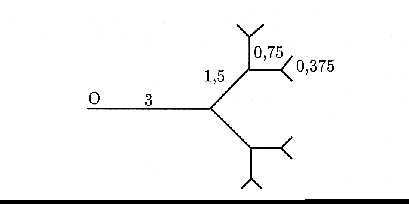
Ecrire une action de tracé d'un arbre binaire. Les données sont la profondeur de l'arbre et le point origine, la taille et le cap du tronc. Par exemple, pour une profondeur 5, et un troncd'origine 0, de taille 3 orienté dans le sens OuestEst, on obtient le dessin de la figure 8.3.

Figure 8.3: Arbre binaire de profondeur 5

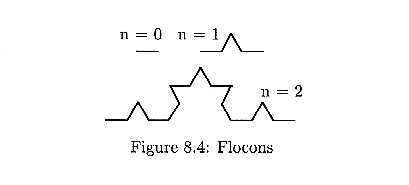
E8.7 : Flocons

Définir une action de tracé de dessins de la famille donnée par la figure 8.4. Les données sont la taille du trait élémentaire et le nombre de niveaux.

E8.8 : Etoiles

L'objet de cet exercice est de construire un algorithme de tracé d'un dessin récursif formé d'étoiles à cinq branches, comme l'illustrent les deux figures 8.5 et 8.6.

Figure 8.5: Etoiles à cinq branches

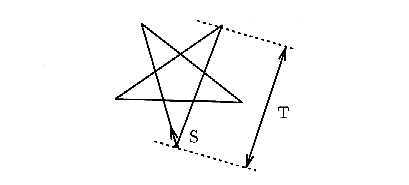
Q1) Tracé d'une étoile à cinq branches

On veut tracer une étoile à cinq branches comme celle de la figure 8.5. Une telle étoile est caractérisée par :

• son sommet (S sur la figure 8.5) : c'est l'un des sommets (points extrêmes) de l'étoile
• sa taille (T sur la figure 8.5) : c'est la taille commune de tous les segments reliant deux sommets de l'étoile
• son cap (marqué par un vecteur sur la figure 8.5) : c'est le cap de l'un des segments passant par le sommet de l'étoile, et tel qu'un observateur placé au sommet et regardant dans le sens défini par ce cap, voit l'autre extrémité du segment devant lui et le deuxième segmentpassant par le sommet à sa droite. On propose l'action suivante :

TracerUneEtoile (T)

• Quelle est la valeur de l'angle A apparaissant dans l'algorithme ?
• Compléter la spécification de l'action TracerUneEtoile en ce qui concerne l'état de la plume.

On veut maintenant tracer les dessins récursifs composés d'étoiles comme ceux donnés dans la figure 8.6.

 

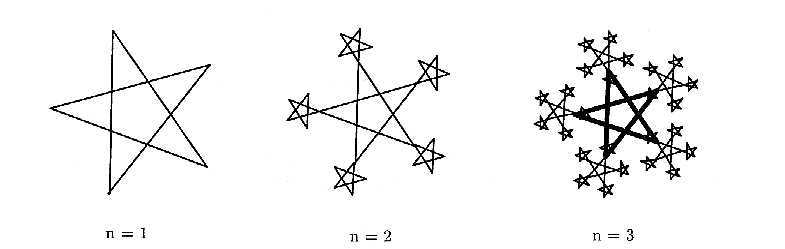
- son ordre, comme le suggèrent les figures : la figure d'ordre I comporte une étoile, la figure d'ordre 2 comporte une étoile de taille T et cinq étoiles de taille T/3, placées à chacun de ses sommets, ...

• son sommet, sa taille, son cap : ce sont le sommet, la taille et le cap de l'étoile la plus grande.

tracer le dessin de taille T et d'ordre n, sachant qu'à l'état initial, la position dans le plan et le cap de la plume sont respectivement le sommet et le cap du dessin que l'on veut tracer.

E8.9 : Tricot (suite)

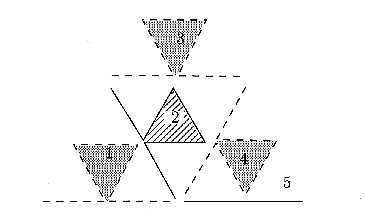
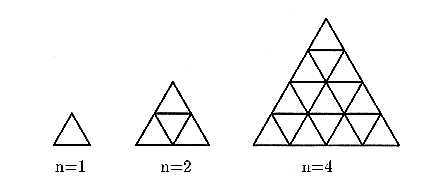
On considère un triangle équilatéral pavé de triangles équilatéraux élémentaires (figure 8.7). Le dessin est caractérisé par un sommet du triangle extérieur, un cap, la taille du coté du triangle extérieur et le nombre n de divisions en traits élémentaires du côté du triangle extérieur (n est une puissance de 2).

On spécifie l'action Ttriangles :

Figure 8.7: Triangles équilatéraux

Indications :

On peut envisager deux solutions :

- On décompose la figure en distinguant deux des côtés du triangle extérieur. Ces deux segments ne font pas partie de l'analyse récurrente. La figure intérieure restante doit être analysée récursivement. On peut y voir 4 objets numérotés 1, 2, 3 et 4, et un segment numéroté 5, comme suggéré figure 8.8. Les quatre objets 1, 2, 3, et 4 peuvent être tracés par une action récursive intermédiaire que l'on spécifiera.

- On décompose la figure en distinguant le triangle extérieur et l'intérieur de la figure. La figure intérieure doit être analysée récursivement. On peut la voir comme suggéré figure 8.9.

Figure 8.8: Triangles équilatéraux: indications pour le tracé récursif,solution1

Figure 8.9: Triangles équilatéraux: indications pour le tracé récursif,solution2