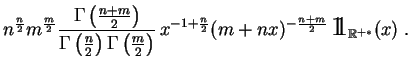![$\displaystyle P[X\in A] = \int_A f_X(x)\,dx\;.
$](img336.gif)
![$\displaystyle P[X\in A] = \int_A f_X(x)\,dx\;.
$](img336.gif)
Pour déterminer la loi d'une
variable aléatoire continue,
il faut donc
calculer sa
densité.
De manière équivalente, on détermine la loi
d'une
variable continue
en donnant la
probabilité
qu'elle appartienne
à un intervalle ![]() quelconque. C'est ce que nous avions fait pour
notre exemple de base, l'appel de
Random,
qui est une
variable aléatoire continue,
de densité
1
quelconque. C'est ce que nous avions fait pour
notre exemple de base, l'appel de
Random,
qui est une
variable aléatoire continue,
de densité
1![]() .
.
Une
variable aléatoire continue
![]() , de
densité
, de
densité
![]() , tombe entre
, tombe entre
![]() et
et ![]() avec une
probabilité
égale à :
avec une
probabilité
égale à :
![$\displaystyle P[a<X < b]=\int_{a}^b\,f_X(x)\,dx\;.
$](img340.gif)
Comme nous l'avons déjà observé pour Random , la probabilité pour une variable aléatoire continue, de tomber sur un point quelconque est nulle.
![$\displaystyle P[X=a] = \int_{\{a\}} f_X(x)\,dx = 0\;.
$](img341.gif)
Comme dans le cas discret quelques exemples de base sont à connaître.
Loi uniforme.
La loi uniforme sur un intervalle est la loi des "tirages
au hasard"
dans cet intervalle. Si ![]() sont deux réels, la loi uniforme
sur l'intervalle
sont deux réels, la loi uniforme
sur l'intervalle ![]() est notée
est notée
![]() . Elle a pour
densité
:
. Elle a pour
densité
:
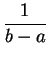 1
1
Loi exponentielle.
Les
lois exponentielles
modélisent des durées
aléatoires,
comme des durées de vie de particules en physique. La
loi exponentielle
de paramètre
![]() est notée
est notée
![]() .
Elle a pour
densité
:
.
Elle a pour
densité
:
Loi normale.
La loi normale,
loi de Gauss,
ou de
Laplace-Gauss,
est la
plus célèbre des
lois de probabilité.
Son succès, et son
omniprésence
dans les sciences de la vie, viennent du
théorème central limite
que nous
étudierons plus loin. La
loi normale
de paramètres
![]() et
et
![]() est notée
est notée
![]() . Elle a pour
densité
:
. Elle a pour
densité
:
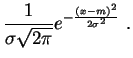
Les lois exponentielles et normales sont au centre des familles de lois classiques, qui sont les plus fréquemment rencontrées en statistiques.
Loi de Weibull.
La
loi de Weibull
de paramètres ![]() et
et
![]() , notée
, notée
![]() a pour
densité
:
a pour
densité
:
Loi gamma.
La
loi gamma
de paramètres ![]() et
et
![]() , notée
, notée
![]() a pour
densité
:
a pour
densité
:
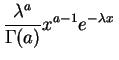 1
1
Pour ![]() entier,
entier, ![]() et
et
![]() , la loi
, la loi
![]() est
appelée
loi de chi-deux
à
est
appelée
loi de chi-deux
à ![]() degrés de liberté, et notée
degrés de liberté, et notée
![]() . C'est la loi de la somme
des carrés de
. C'est la loi de la somme
des carrés de ![]() variables aléatoires indépendantes
de loi
variables aléatoires indépendantes
de loi
![]() . On l'utilise pour les
variances empiriques
d'échantillons
gaussiens.
La loi
. On l'utilise pour les
variances empiriques
d'échantillons
gaussiens.
La loi
![]() est la
loi exponentielle
est la
loi exponentielle
![]() .
.
Loi béta.
La
loi béta
de paramètres ![]() et
et
![]() , notée
, notée
![]() a pour
densité
:
a pour
densité
:
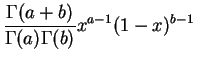 1
1
Cette famille fournit des modèles non uniformes pour des variables
aléatoires bornées. Si des
variables aléatoires indépendantes
suivent la
loi uniforme
![]() , leurs
statistiques d'ordre
(valeurs réordonnées) suivent des
lois béta.
, leurs
statistiques d'ordre
(valeurs réordonnées) suivent des
lois béta.
Loi log-normale.
La
loi log-normale
![]() est la loi
d'une
variable aléatoire
à valeurs positives, dont le logarithme suit
la loi
est la loi
d'une
variable aléatoire
à valeurs positives, dont le logarithme suit
la loi
![]() . Elle a pour
densité
:
. Elle a pour
densité
:
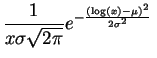 1
1
Loi de Student.
La
loi de Student
à ![]() degrés de liberté,
degrés de liberté,
![]() est la loi du rapport
est la loi du rapport
![]() , où les
variables aléatoires
, où les
variables aléatoires
![]() et
et ![]() sont
indépendantes
,
sont
indépendantes
, ![]() de loi
de loi
![]() ,
,
![]() de loi
de loi
![]() . Elle a pour
densité
:
. Elle a pour
densité
:
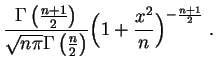
Loi de Fisher. La
loi de Fisher
de paramètres
![]() et
et
![]() (entiers positifs), est la loi du rapport
(entiers positifs), est la loi du rapport
![]() , où
, où ![]() et
et ![]() sont deux
variables aléatoires indépendantes,
de lois respectives
sont deux
variables aléatoires indépendantes,
de lois respectives
![]() et
et
![]() . Elle a pour
densité
:
. Elle a pour
densité
: